Значения тригонометрических функций
Ключевые слова: радиан, радианная мера угла, тригонометрическая окружность, знаки тригонометрических функций
В геометрии угол определяется как часть плоскости, ограниченная двумя лучами.
При таком определении получаются углы от 0° до 180°. Однако угол можно рассматривать и как меру поворота.
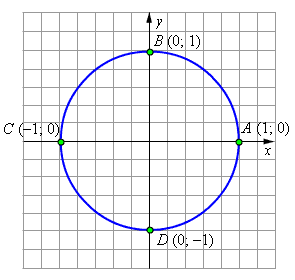
Возьмем на координатной плоскости окружность радиуса R с центром O в начале координат.
Пусть одна сторона угла $$\alpha$$ с вершиной в начале координат O идет по оси абсцисс, а сам угол положительный, то есть, по определению, отложен по направлению против часовой стрелки от положительного направления оси абсцисс.
Из геометрии известно, что отношение длины дуги l , на которую опирается этот угол, к радиусу R этой окружности не зависит от самого радиуса. Поэтому это отношение может быть выбрано характеристикой и мерой данного угла: $$\alpha = \frac{l}{R}$$.
Такая мера называется радианной мерой угла и используется наравне с угловой.
Говорят, что угол равен определенному числу радиан.
Ясно, что угол в один радиан опирается на длину дуги окружности, равную её радиусу.
В самом деле: $$\alpha = \frac{R}{R} = 1$$ радиан. Обозначение радиана – «рад».
Так как длина всей окружности радиуса R равна 2$$\pi$$R , то всей окружности соответствует угол $$\alpha = \frac{2\pi R}{R} = 2\pi $$ радиан. Поскольку вся окружность содержит 360°, то один радиан соответствует $$\frac{360^\circ}{2\pi}= \frac{180^\circ}{\pi}$$ градусов:
$$1 рад = \frac{180^\circ}{\pi}\simeq57,17^\circ$$. И наоборот, $$1^\circ = \frac{\pi}{180}рад$$.
Значит, можно написать следующие формулы перехода от градусного измерения к радианному:
$$\alpha = \frac{\pi\alpha^\circ}{180^\circ} рад$$
и от радианного измерения к градусному:
$$\alpha^\circ = \frac{180^\circ}{\pi}\alpha$$.
Обозначение «рад» при записи часто опускают и вместо, например, 180° = $$\pi$$ рад пишут просто 180° = $$\pi$$.
Пользуясь этими формулами, легко получить следующую таблицу перевода некоторых наиболее часто встречающихся углов из градусной меры в радианную и обратно.
|
Угол, градусы |
0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
|
Угол, радианы |
0 | $$\frac{\pi}{6}$$ |
$$\frac{\pi}{4}$$ |
$$\frac{\pi}{3}$$ |
$$\frac{\pi}{2}$$ |
$$\pi$$ |
$$\frac{3\pi}{2}$$ |
$$2\pi$$ |
Так как, синус по определению равен ординате точки на единочной окружности, а косинус - абсциссе, то знаки тригонометрических функций по четвертям будут такими:
| I |
II |
III |
IV |
|
| $$sin\alpha$$ | + |
+ |
- | - |
| $$cos\alpha$$ |
+ |
- | - | + |
| $$tg\alpha$$ |
+ |
- | + |
- |
| $$ctg\alpha$$ |
+ |
- | + |
- |
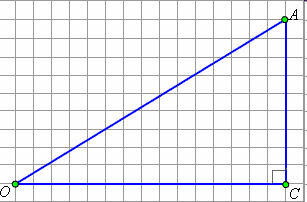
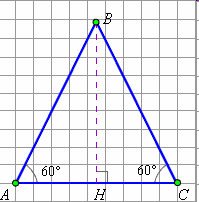
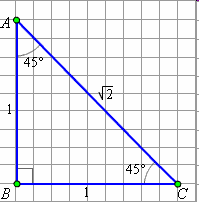
Вычисление тригонометрических функций некоторых углов.
|
|
 |
 |
 |