Квадратичные неравенства

Квадратичное неравенство. Квадратичным неравенством называется неравенство вида $$ f(x) \vee 0
$$, где $$ f(x) = ax^2 + bx + c$$ и $$ a \ne 0$$.

Замечание. Знак $$ \vee $$ подразумевает один из знаков: $$< ,\; > ,\; \le ,\; \ge $$.

Пусть $$ D = b^2 - 4ac$$ и $$ x_1 < x_2 $$ - корни f(x).


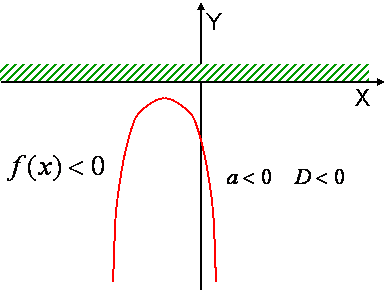
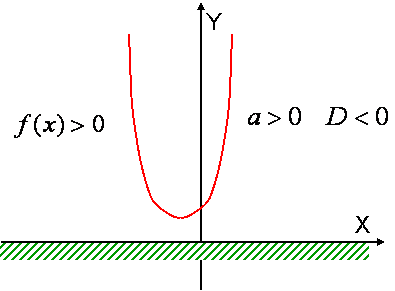
Теорема 1. Если $$ a < 0$$ и $$D < 0$$, то для всех x выполняется неравенство $$f(x) < 0$$	Теорема 2. Если $$ a > 0$$ и $$D < 0$$, то для всех x выполняется неравенство $$f(x) > 0$$


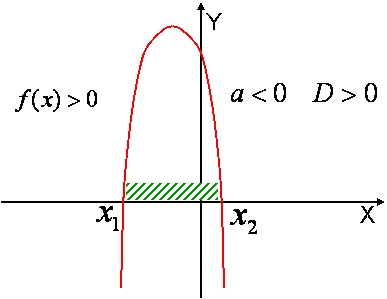
Теорема 3. Если $$ a < 0$$ и $$D >0$$, то для всех $$ x \in \left( {x_1 ;x_2 } \right)$$ выполняется неравенство $$f(x) > 0$$, а для всех $$x \in \left( { - \infty ;x_1 } \right) \cup \left( {x_2 ; + \infty } \right)$$ выполняется неравенство $$f(x) < 0$$.


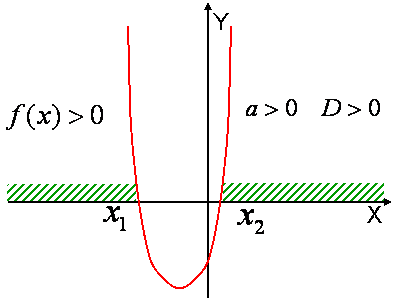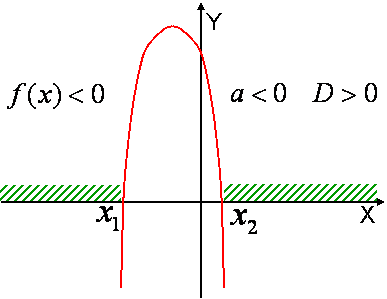
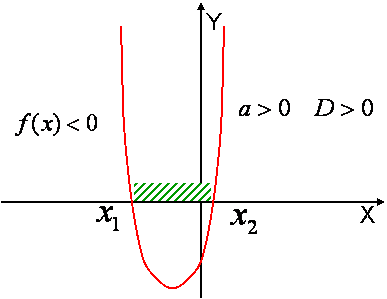
Теорема 4. Если $$ a > 0$$ и $$D >0$$, то для всех $$ x \in \left( {x_1 ;x_2 } \right)$$ выполняется неравенство $$f(x) < 0$$, а для всех $$x \in \left( { - \infty ;x_1 } \right) \cup \left( {x_2 ; + \infty } \right)$$ выполняется неравенство $$f(x) >0$$.


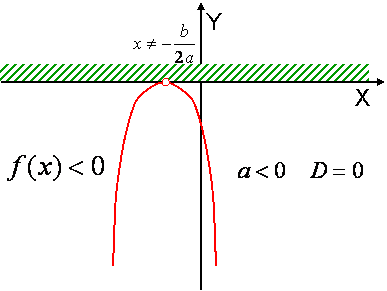
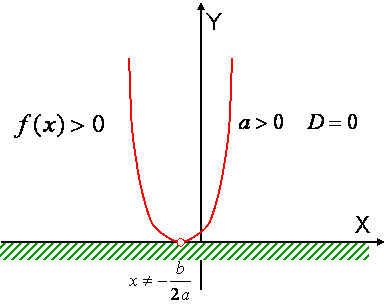
Теорема 5. Если $$ a < 0$$ и D = 0 , то для всех $$ x \ne - \frac{b}{{2a}}$$ выполняется неравенство $$f(x) < 0$$	Теорема 6. Если $$ a > 0$$ и D = 0 , то для всех $$ x \ne - \frac{b}{{2a}}$$ выполняется неравенство $$f(x) > 0$$